Video: Ինչպե՞ս եք օգտագործում զրոյական արտադրանքի հատկությունը:
2024 Հեղինակ: Miles Stephen | [email protected]. Վերջին փոփոխված: 2023-12-15 23:37
Այն Զրո արտադրանքի հատկություն նշում է, որ եթե ab = 0, ապա կամ a = 0 կամ b = 0, կամ երկուսն էլ a և b են 0: Երբ արտադրանքը գործոնների հավասար զրո , գործոններից մեկը կամ մի քանիսը նույնպես պետք է հավասար լինեն զրո . Երբ բազմանդամը գործոնավորվում է, յուրաքանչյուր գործակից սահմանեք հավասար զրո և դրանք լուծել առանձին:
Հաշվի առնելով սա՝ ինչպե՞ս է աշխատում զրոյական արտադրանքի հատկությունը:
Այն Զրո արտադրանքի հատկություն . Այն Զրո արտադրանքի հատկություն պարզապես նշում է, որ եթե ab=0, ապա կամ a=0 կամ b=0 (կամ երկուսն էլ): Ա արտադրանքը գործոններից է զրո եթե և միայն այն դեպքում, երբ գործոններից մեկը կամ մի քանիսն են զրո . Սա հատկապես օգտակար է քառակուսի հավասարումներ լուծելիս:
Ավելին, ի՞նչ է նշանակում բաշխիչ սեփականություն: Այն բաշխիչ սեփականությունն է ամենահաճախ օգտագործվողներից մեկը հատկությունները մաթեմատիկայի մեջ։ Ընդհանուր առմամբ, այս տերմինը վերաբերում է բաշխիչ սեփականություն բազմապատկման, որը նշում է, որ. Սահմանում : The բաշխիչ սեփականություն թույլ է տալիս բազմապատկել գումարը` բազմապատկելով յուրաքանչյուր հավելում առանձին, այնուհետև ավելացնել արտադրյալները:
Այս կերպ, ինչու՞ 0-ը չի կարող լինել քառակուսի հավասարման մեջ:
Եթե քառակուսի հավասարում ax^2+bx+c= 0 ունի ավելի քան երկու արմատ, ապա այն դառնում է ինքնություն a=b=c= 0 . Հենց որ «ա = 0 «Դուք այլևս 2-րդ աստիճան չունեք հավասարումը . Եվ ձեր գրաֆիկը պարաբոլա չի լինի: Եթե a=b=c= 0 , ապա ձախ կողմը հավասարումը դառնում է 0.
Ո՞րն է զրոյի բազմապատկման հատկությունը:
Այն բազմապատկման հատկություն նշում է, որ ցանկացած թվի արտադրյալ և զրո է զրո . Կարևոր չէ, թե որ թիվն է, երբ այն բազմապատկես զրո , Դուք ստանում եք զրո որպես պատասխան.
Խորհուրդ ենք տալիս:
Ինչպե՞ս լուծել քառակուսի հավասարումը՝ օգտագործելով զրոյական գործոնի օրենքը:
Այստեղից կարող ենք եզրակացնել, որ եթե ցանկացած երկու թվի արտադրյալը զրո է, ապա թվերից մեկը կամ երկուսը զրո են: Այսինքն, եթե ab = 0, ապա a = 0 կամ b = 0 (որը ներառում է հնարավորություն, որ a = b = 0): Սա կոչվում է զրոյական գործոնի օրենք; և մենք հաճախ օգտագործում ենք այն քառակուսի հավասարումներ լուծելու համար
Ինչպե՞ս եք հաշվարկում Pearson արտադրանքի պահերի հարաբերակցությունը SPSS-ում:
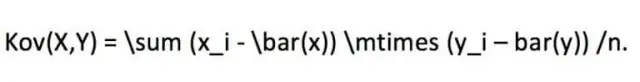
Երկփոփոխական Pearson հարաբերակցությունը գործարկելու համար սեղմեք Վերլուծել > Հարաբերակցել > Երկփոփոխություն: Ընտրեք Height և Weight փոփոխականները և տեղափոխեք դրանք Փոփոխականներ տուփ: Հարաբերակցության գործակիցների տարածքում ընտրեք Pearson: Նշանակության թեստում ընտրեք ձեր ուզած նշանակության թեստը՝ երկպոչ կամ միապոչ
Ինչպե՞ս եք օգտագործում աջ ձեռքի կանոնը խաչաձև արտադրանքի համար:
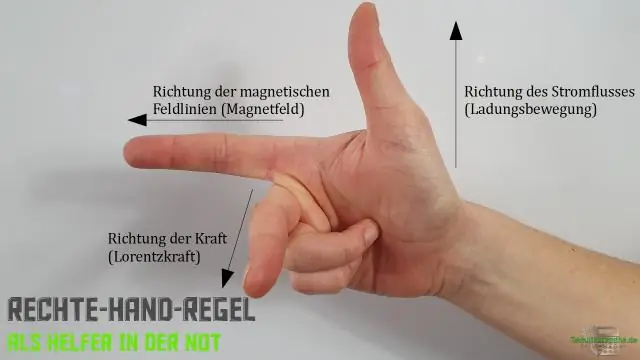
Աջ ձեռքի կանոնը սահմանում է, որ վեկտորների խաչաձև արտադրյալի կողմնորոշումը որոշվում է՝ դնելով և պոչից պոչը՝ հարթեցնելով աջ ձեռքը, երկարացնելով այն դեպի ուղղությամբ և այնուհետև ոլորելով մատները այն ուղղությամբ, որով կազմում է անկյունը: Բութ մատն այնուհետև ուղղված է դեպի
Ինչպե՞ս եք փոխակերպում գործակիցի կանոնը արտադրանքի կանոնի:
Քվեարկության կանոնը կարող է դիտվել որպես արտադրանքի և շղթայի կանոնների կիրառում: Եթե Q(x) = f(x)/g(x), ապա Q(x) = f(x) * 1/(g(x)): Դուք կարող եք օգտագործել արտադրանքի կանոնը Q(x) տարբերակելու համար, իսկ 1/(g(x))-ը կարելի է տարբերակել՝ օգտագործելով շղթայի կանոնը u = g(x), և 1/(g(x)) = 1/u:
Ինչպե՞ս լուծել հավասարության գումարման հատկությունը:
Հավասարության գումարման հատկություն Եթե երկու արտահայտություն հավասար են միմյանց, և դուք նույն արժեքը ավելացնեք հավասարման երկու կողմերին, ապա հավասարումը կմնա հավասար: Երբ դուք լուծում եք հավասարումը, դուք գտնում եք այն փոփոխականի արժեքը, որը դարձնում է հավասարումը ճշմարիտ: Հավասարումը լուծելու համար դուք մեկուսացնում եք փոփոխականը