Video: Ո՞ր trig ֆունկցիաներն ունեն pi-ի ժամանակաշրջան:
2024 Հեղինակ: Miles Stephen | [email protected]. Վերջին փոփոխված: 2023-12-15 23:37
Բոլոր չորս ֆունկցիաները պարբերական են՝ շոշափող և կոտանգենս ունեն π ժամանակահատված, մինչդեռ կոսեկանտը և սեկանտը ունեն 2π պարբերություն:
Բացի դրանից, ի՞նչ ֆունկցիա ունի pi-ի ժամանակաշրջանը:
Ինչպես տեսնում եք, շոշափող ունի պ–ի շրջան , յուրաքանչյուրի հետ ժամանակաշրջան բաժանված ուղղահայաց ասիմպտոտով:
Բացի այդ, Կոտանգենսն ունի՞ պի պարբերություն: Այն հատված և կոսեսանտ ունեն ժամանակաշրջաններ 2π երկարությամբ, և մենք չենք դիտարկում այս կորերի ամպլիտուդությունը: Այն Կոտանգենսն ունի π պարբերություն , և մենք չենք անհանգստացնում ամպլիտուդով:
Երկրորդ, ո՞րն է պի-ի ժամանակաշրջանը:
սովորական ժամանակաշրջան 2 է պ , բայց մեր դեպքում դա «արագացվում է» (կարճացնում է) 4-ը 4x-ով, ուստի Ժամանակաշրջան = պ /2.
Ինչպե՞ս գտնել տրիգ ֆունկցիայի ժամանակաշրջանը:
Եթե ձեր trig ֆունկցիան կա՛մ շոշափող է, կա՛մ կոտանգենս, ապա դուք պետք է բաժանեք pi-ն ձեր B-ի բացարձակ արժեքի վրա: ֆունկցիան , f(x) = 3 sin(4x + 2), a սինուսային ֆունկցիա , այնպես որ ժամանակաշրջան կլինի 2 pi բաժանված 4-ի, մեր B արժեքը:
Խորհուրդ ենք տալիս:
Ինչու են հանքանյութերը տարբեր բյուրեղային ձևեր ունեն:
Հանքային բյուրեղները ձևավորվում են տարբեր ձևերի և չափերի: Հանքանյութը կազմված է ատոմներից և մոլեկուլներից։ Երբ ատոմներն ու մոլեկուլները միավորվում են, նրանք ձևավորում են որոշակի օրինաչափություն: Հանքանյութի վերջնական ձևն արտացոլում է սկզբնական ատոմային ձևը
Ի՞նչ 3 ընդհանուր բան ունեն բոլոր բջիջները:
Կենդանի էակների բոլոր բջիջներն ունեն երեք ընդհանուր բան՝ ցիտոպլազմա, ԴՆԹ և պլազմային թաղանթ։ Յուրաքանչյուր բջիջ պարունակում է ջրի վրա հիմնված մատրիցա, որը հայտնի է որպես ցիտոպլազմա և ընտրովի թափանցելի բջջային թաղանթ: Բոլոր բջիջները կազմված են ԴՆԹ-ից, նույնիսկ եթե չունեն միջուկ
Ինչպե՞ս գտնել trig ֆունկցիայի երկրորդ ածանցյալը:
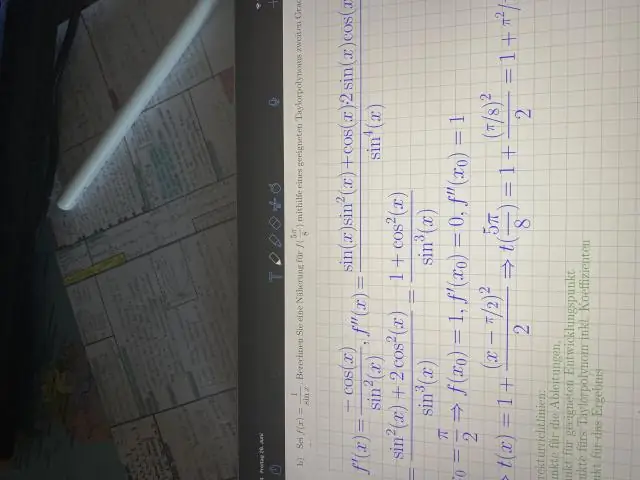
ՏԵՍԱՆՅՈՒԹ Այսպիսով, որո՞նք են 6 trig ֆունկցիաների ածանցյալները: Եռանկյունաչափական ֆունկցիաների ածանցյալներ. Հիմնական եռանկյունաչափական ֆունկցիաները ներառում են հետևյալ 6 ֆունկցիաները. մեղք x), կոսինուս ( cos x), շոշափող (tanx), կոտանգենս (cotx), secant (secx) և cosecant (cscx):
Ի՞նչ է նշանակում չորրորդական ժամանակաշրջան:
Չորրորդական շրջանը երկրաբանական ժամանակաշրջան է, որն ընդգրկում է ամենավերջին 2,6 միլիոն տարին, ներառյալ մեր օրերը: Այդ ժամանակաշրջանը տեսավ նաև նոր գիշատիչի՝ մարդու առաջացումը
Ի՞նչ է նշանակում չորրորդական ժամանակաշրջան աշխարհագրության մեջ:
Չորրորդական շրջանը երկրաբանական ժամանակաշրջան է, որն ընդգրկում է ամենավերջին 2,6 միլիոն տարին, ներառյալ մեր օրերը: Չորրորդական շրջանը ներառում էր կլիմայի կտրուկ փոփոխություններ, որոնք ազդեցին սննդի պաշարների վրա և բերեցին բազմաթիվ տեսակների անհետացման։