
- Հեղինակ Miles Stephen stephen@answers-science.com.
- Public 2024-01-18 08:16.
- Վերջին փոփոխված 2025-01-22 17:01.
Այն Ժամանակաշրջան անցնում է մի գագաթից մյուսը (կամ ցանկացած կետից հաջորդ համապատասխան կետ). Լայնություն բարձրությունն է կենտրոնական գծից մինչև գագաթը (կամ մինչև տաշտը):
Այժմ մենք կարող ենք տեսնել.
- ամպլիտուդություն A = 3 է:
- ժամանակաշրջան կազմում է 2π/100 = 0,02 պ
- փուլային տեղաշարժը C = 0,01 է (դեպի ձախ)
- ուղղահայաց տեղաշարժը D = 0 է:
Նաև գիտեք, թե ինչպես եք գտնում գրաֆիկի պարբերությունը:
Այն ժամանակաշրջան սինուսի կորը կորի մեկ շրջանի երկարությունն է: Բնականը ժամանակաշրջան սինուսի կորը 2π է: Այսպիսով, b=1 գործակիցը համարժեք է a-ին ժամանակաշրջան of2π. ստանալու համար ժամանակաշրջան սինուսի կորի ցանկացած b գործակցի համար, պարզապես 2π բաժանեք b գործակցի վրա, որպեսզի ստացվի նոր ժամանակաշրջան կորի.
ո՞րն է ժամանակաշրջանի բանաձևը. Այն բանաձեւ ժամանակի համար՝ T ( ժամանակաշրջան ) = 1 / f (հաճախականություն): Այն բանաձեւ ալիքի երկարության համար λ (m) =c / f է: λ = c / f = ալիքի արագություն c (մ / վ) / հաճախականություն f (Հց): Հերց միավորը (Հց) ժամանակին կոչվում էր cps = ցիկլեր վայրկյանում:
Համապատասխանաբար, ինչպե՞ս եք գտնում սինուսի գրաֆիկի հորիզոնական տեղաշարժը:
Սինուսոիդայինից հավասարումը , է հորիզոնական տեղաշարժ ստացվում է որոշող փոփոխությունը կատարվում է x արժեքի վրա: Որոշելու ամենահեշտ ձևը հորիզոնական տեղաշարժ է որոշել, թե քանի միավորով է ստանդարտի «մեկնարկային կետը» (0, 0): սինուսային կոր , y = sin(x), տեղափոխվել է աջ կամ ձախ:
Արդյո՞ք ամպլիտուդը միշտ դրական է:
Լայնություն . Ամպլիտուդներ են միշտ դրական թվեր (օրինակ՝ 3.5, 1, 120) և երբեք բացասական չեն (օրինակ՝ -3.5, -1, -120): Ամպլիտուդներ են դրական քանի որ հեռավորությունը կարող է լինել միայն զրոյից մեծ կամ հավասար զրոյի; բացասական հեռավորություն գոյություն չունի.
Խորհուրդ ենք տալիս:
Ինչպե՞ս է չափվում երկայնական ալիքի ամպլիտուդը:
Լայնակի ալիքում ամպլիտուդը չափում է հանգստի դիրքից մինչև գագաթը (ալիքի բարձր կետը) կամ մինչև ալիքը (ալիքի ցածր կետ): Երկայնական ալիքում, ինչպես այս տեսանյութը, ամպլիտուդը չափվում է որոշելով. որքանով են հեռացել միջավայրի մոլեկուլները իրենց սովորական հանգստի դիրքից
Ինչպե՞ս գտնել գրաֆիկի մայր ֆունկցիան:

Օրինակ, դուք կարող եք պարզեցնել 'y=2*sin(x+2)'-ը 'y=sin(x)' կամ 'y=|3x+2|' դեպի 'y=|x|.' Գծապատկերե՛ք արդյունքը։ Սա ծնող գործառույթն է: Օրինակ՝ «y=x^+x+1»-ի մայր ֆունկցիան պարզապես «y=x^2» է, որը նաև հայտնի է որպես քառակուսի ֆունկցիա։
Ինչպե՞ս գտնել գրաֆիկի հարաբերակցությունը:

Գծեք ամբողջ գծապատկերի ընդհանուր թիվը մեկ տողի կամ գծի թվով, որպեսզի ձեզ տրվի բարակ կամ գծային գծապատկերի հարաբերակցությունը: Օրինակ, եթե գծապատկերում գծապատկերը ներկայացնում է 5-ը՝ ընդհանուր 30-ով, դուք 30-ը կբաժանեք 5-ի: Դա ձեզ կտա 6-ի արդյունք: Հետևաբար, հարաբերակցությունը կլինի 6:1:
Ինչպե՞ս գտնել գրաֆիկի երկու կետերի միջև հեռավորությունը:
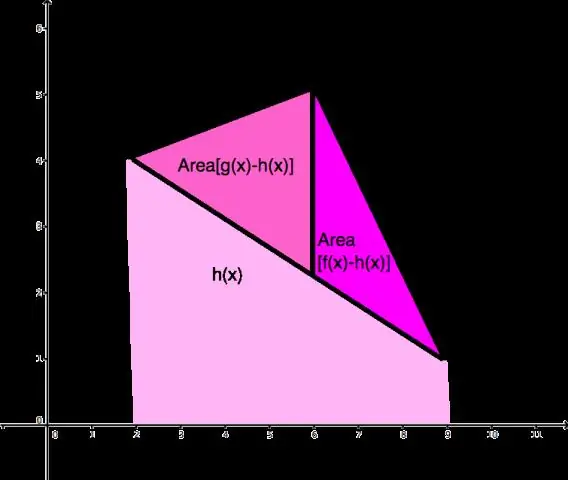
Քայլեր Վերցրեք երկու կետերի կոորդինատները, որոնց միջև հեռավորությունը պետք է գտնել: Մի կետն անվանեք 1 կետ (x1,y1), իսկ մյուսը դարձրեք 2 կետ (x2,y2): Իմացեք հեռավորության բանաձևը. Գտեք կետերի միջև հորիզոնական և ուղղահայաց հեռավորությունը: Երկու արժեքների քառակուսի: Միասին ավելացրեք քառակուսի արժեքները: Վերցրեք հավասարման քառակուսի արմատը
Ինչպե՞ս գտնել միջին արագությունը արագության ընդդեմ ժամանակի գրաֆիկի վրա:

Արագություն/ժամանակ կորի տակ գտնվող տարածքը ընդհանուր տեղաշարժն է: Եթե դա բաժանեք ժամանակի փոփոխության վրա, ապա կստանաք միջին արագությունը: Արագությունը արագության վեկտորային ձևն է: Եթե արագությունը միշտ ոչ բացասական է, ապա միջին արագությունը և միջին արագությունը նույնն են
