Video: Կարո՞ղ է արդյոք ինտեգրալ թեստն ապացուցել տարաձայնությունը:
2024 Հեղինակ: Miles Stephen | [email protected]. Վերջին փոփոխված: 2023-12-15 23:37
Օրինակ 1 Որոշեք, արդյոք հետևյալ շարքը կոնվերգենտ է կամ տարբերվող . Այս ֆունկցիան ակնհայտորեն դրական է, և եթե x x-ը մեծացնենք հայտարարը կամք դառնում են ավելի մեծ, և այդպիսով ֆունկցիան նույնպես նվազում է: Այն անբաժանելի է տարբերվող և այսպես, շարքը նույնպես տարբերվող միջոցով Ինտեգրալ թեստ.
Բացի սրանից, e x-ը կոնվերգենտ է, թե դիվերգենտ:
1/( նախկին ) ավելի մեծ է կամ հավասար 1/( նախկին +1) (զրոյի և անսահմանի միջև) Անպատշաճ ինտեգրալ ∫∞01( նախկին ) դ x է կոնվերգենտ և դա 1 է, սակայն, ոչ պատշաճ ինտեգրալ ∫∞01( նախկին +1) դ x է տարբերվող.
Կարելի է նաև հարցնել՝ ո՞րն է օրինակով ոչ պատշաճ ինտեգրալը։ Ան ոչ պատշաճ ինտեգրալ միանշանակ է անբաժանելի որն ունի մեկ կամ երկու սահմաններ անսահման կամ ինտեգրալ, որը մոտենում է անսահմանությանը ինտեգրման միջակայքի մեկ կամ մի քանի կետերում: Անպատշաճ ինտեգրալներ չի կարող հաշվարկվել սովորական Riemann-ի միջոցով անբաժանելի . Համար օրինակ , է անբաժանելի.
Երկրորդ, ի՞նչ է համընկնումն ու դիվերգենցիան հաշվում:
Սերիա Կոնվերգենցիա և տարաձայնություն - Սահմանումներ A շարք Σa համընկնում է S գումարին, եթե և միայն այն դեպքում, եթե մասնակի գումարների հաջորդականությունը համընկնում է S-ին: Այսինքն, շարքը զուգակցվում է, եթե գոյություն ունի հետևյալ սահմանը. Հակառակ դեպքում, եթե s-ի սահմանըկ (քանի որ k → ∞) անսահման է կամ գոյություն չունի, այնուհետև շարքը շեղվում է:
Որքա՞ն է 1 անսահմանության արժեքը:
Ըստ էության, 1 շատ մեծ թվով բաժանվածը շատ մոտ է զրոյին, ուստի… 1 բաժանված անսահմանություն , եթե իրականում կարողանայիք հասնել անսահմանություն , հավասար է 0-ի։
Խորհուրդ ենք տալիս:
Կարո՞ղ է արդյոք մարմինն առանց էներգիայի թափ ունենալ:
Պատասխան և բացատրություն. Մարմինը չի կարող իմպուլս ունենալ առանց էներգիա ունենալու: Դա պայմանավորված է նրանով, որ միայն շարժվող առարկաներն ունեն շարժ, իսկ շարժման մեջ գտնվող առարկաները միշտ ունեն շարժունակ
Կարո՞ղ են արդյոք A և B արյան խմբեր ունեցող ծնողները O-ով երեխա ունենալ:
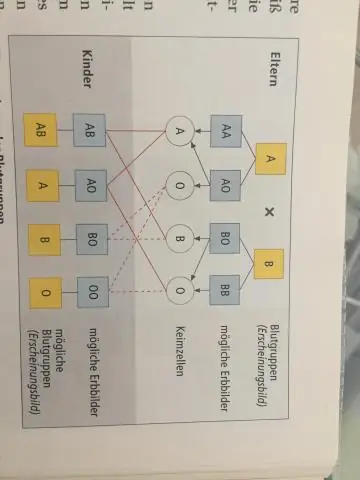
Այո, քանի որ յուրաքանչյուր մարդ ունի արյան խմբի երկու «գեն»: Հետևաբար, A կամ B արյան խումբ ունեցող երկու ծնողներ կարող են ծնել O արյան խումբ ունեցող երեխա: Եթե նրանք երկուսն էլ ունեն AO կամ BO գեներ, յուրաքանչյուր ծնող կարող է ժառանգներին նվիրաբերել O գեն: Այնուհետև սերունդները կունենան OO գեներ, ինչը նրանց կդարձնի արյան O խումբ
Կարո՞ղ է արդյոք ինֆրակարմիր սպեկտրոսկոպիան հայտնաբերել կեղտերը:
Ինֆրակարմիր սպեկտրոսկոպիան օգտագործվում է հետազոտության մեջ՝ նմուշները հայտնաբերելու, քանակական վերլուծություններ կատարելու կամ կեղտերը հայտնաբերելու համար: Ինֆրակարմիր սպեկտրոսկոպիան կարող է օգտագործվել գազային, հեղուկ կամ պինդ նմուշների վրա և չի ոչնչացնում նմուշը գործընթացում
Ի՞նչ է նշանակում ինտեգրալ:
Ինչ-որ բան, որն անբաժանելի է, շատ կարևոր է կամ անհրաժեշտ: Եթե դու թիմի անբաժան մասն ես, նշանակում է, որ թիմն առանց քեզ չի կարող գործել։ Ինտեգրալը միջին անգլերենից է, միջնադարյան լատիներեն integralis-ից՝ «կազմում է մի ամբողջություն», լատիներեն ամբողջ թվից՝ «untouched, whole»:
Ինչպե՞ս կարող է շերտավոր թեստն օգտակար լինել օգտակար հանածոների հայտնաբերման համար:
«Շերտի թեստը» մեթոդ է, որն օգտագործվում է փոշու տեսքով հանքանյութի գույնը որոշելու համար: Շերտավոր փորձարկումն իրականացվում է հանքանյութի նմուշը քերելով անփայլ ճենապակի կտորի վրա, որը հայտնի է որպես «շերտավոր ափսե»: Սա կարող է արտադրել փոքր քանակությամբ փոշիացված հանքանյութ ափսեի մակերեսին