- Հեղինակ Miles Stephen [email protected].
- Public 2023-12-15 23:37.
- Վերջին փոփոխված 2025-01-22 17:00.
Այն կոտանգենս ունի ժամանակաշրջան π-ի, և մենք չենք անհանգստանում ամպլիտուդիայով:
Այնուհետև ո՞րն է ռադիաններով կոտանգենս ֆունկցիայի պատասխանի ժամանակահատվածը:
Պատասխանել Փորձագետը ստուգել է շոշափողը ֆունկցիան ունի ժամանակաշրջան π-ի կամ 3.14. Այն ժամանակաշրջան այն կետն է, որտեղ գրաֆիկը դիպչում է x առանցքին: Գրաֆիկը անցնում է 0-ով և այնուհետև π. Հաջորդ կետը 2π է:
Նմանապես, ո՞րն է տրիգ ֆունկցիաների ժամանակաշրջանը: Այն ժամանակաշրջան ա ֆունկցիան մեկ ամբողջական ցիկլի հորիզոնական երկարությունն է։ Այն ժամանակաշրջան կարող է նկարագրվել նաև որպես հեռավորություն մեկ «գագաթից» (max) մինչև հաջորդ «գագաթը» (max): Այս սինուսային կորը՝ y = sin x, ունի a ժամանակաշրջան 2π-ից, մեկ ամբողջական ցիկլի հորիզոնական երկարությունը:
Կարելի է նաև հարցնել՝ ինչպե՞ս եք գտնում ֆունկցիայի ժամանակաշրջանը։
Եթե ձեր ձգան ֆունկցիան կա՛մ շոշափող է, կա՛մ կոտանգենս, ապա դուք պետք է բաժանեք pi-ն ձեր B-ի բացարձակ արժեքի վրա: ֆունկցիան , f(x) = 3 sin(4x + 2), սինուս է ֆունկցիան , այնպես որ ժամանակաշրջան կլինի 2 pi բաժանված 4-ի, մեր B արժեքը:
Որքա՞ն է շոշափողի պարբերությունը:
Ինչպես տեսնում եք, որ շոշափող ունի ժամանակաշրջան π-ի, յուրաքանչյուրի հետ ժամանակաշրջան բաժանված ուղղահայաց ասիմպտոտով: «Ամպլիտուդ» հասկացությունն իրականում չի կիրառվում: Գծապատկերների համար նկարեք զրոյականները x = 0, π, 2π և այլն, և ուղղահայաց ասիմպտոների մեջ գծեք յուրաքանչյուր զրոյի միջև ընկած հատվածում:
Խորհուրդ ենք տալիս:
Ո՞րն է քառակուսի ֆունկցիայի հավասարումը:
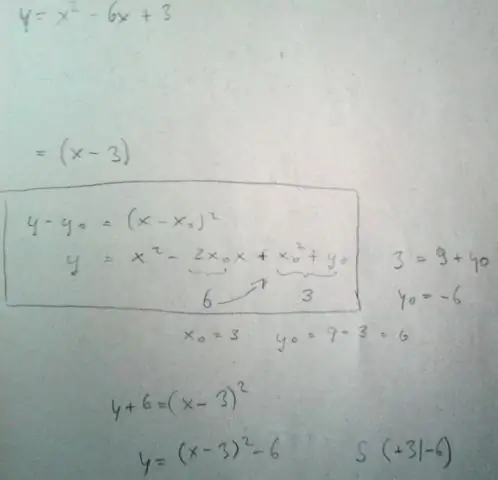
Քառակուսի ֆունկցիան f(x) = ax2 + bx + c ձևերից մեկն է, որտեղ a, b և c թվեր են, որոնց a-ն հավասար չէ զրոյի: Քառակուսային ֆունկցիայի գրաֆիկը կոր է, որը կոչվում է պարաբոլա: Պարաբոլաները կարող են բացվել դեպի վեր կամ վար և տարբեր լինել «լայնությամբ» կամ «կտրուկությամբ», բայց դրանք բոլորն ունեն նույն հիմնական «U» ձևը:
Ի՞նչ է ոչ գծային ֆունկցիայի աղյուսակը:

Ոչ գծային ֆունկցիան այն ֆունկցիան է, որը գծային չէ, իսկ գծային ֆունկցիայի գրաֆիկը գիծ է: Պարզ է, որ y = -x 2 + 4x ֆունկցիայի գրաֆիկը գիծ չէ, ուստի ֆունկցիան ոչ գծային ֆունկցիա է։
Որքա՞ն է էքսպոնենցիալ ֆունկցիայի հակադարձը:
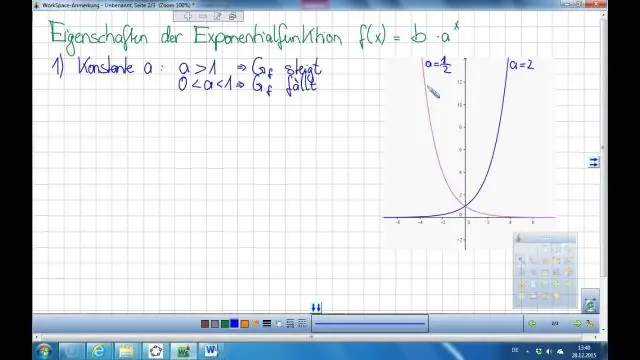
Y = ax էքսպոնենցիոնալ ֆունկցիայի հակադարձը x = ay է: Լոգարիթմական ֆունկցիան y = լոգաքս սահմանվում է որպես համարժեք x = ay էքսպոնենցիալ հավասարմանը
Ո՞րն է օբյեկտիվ ֆունկցիայի գործակիցը:
Գծային ծրագրավորման խնդրի նպատակը կլինի մեծացնել կամ նվազագույնի հասցնել որոշ թվային արժեք: Օբյեկտիվ ֆունկցիայի գործակիցները ցույց են տալիս համապատասխան փոփոխականի մեկ միավորի օբյեկտիվ ֆունկցիայի արժեքի ներդրումը
Ինչպե՞ս է կոչվում առանց տեղումների երկար ժամանակահատվածը:

Երաշտ. գոյական. երկար ժամանակահատված, երբ անձրևը քիչ է կամ ընդհանրապես չկա, և բերքը մեռնում է
