
- Հեղինակ Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:37.
- Վերջին փոփոխված 2025-01-22 17:00.
Մաթեմատիկայի մեջ ան հակադարձ ֆունկցիա (կամ հակա- ֆունկցիան ) է ֆունկցիան որը «շրջում է» մյուսին ֆունկցիան : եթե ֆունկցիան F-ը, որը կիրառվում է x մուտքագրման վրա, տալիս է y-ի արդյունքը, այնուհետև կիրառելով դրա հակադարձ ֆունկցիա g-ից y-ն տալիս է x արդյունքը և հակառակը, այսինքն՝ f(x) = y, եթե և միայն, եթե g(y) = x:
Հետևաբար, ինչպե՞ս կարելի է գտնել ֆունկցիայի հակադարձ հաշվում:
Գտեք ֆունկցիայի հակադարձը
- Նախ, f(x)-ը փոխարինեք y-ով:
- Յուրաքանչյուր x-ը փոխարինիր y-ով և յուրաքանչյուր y-ն փոխարինիր x-ով:
- Լուծեք 2-րդ քայլի հավասարումը y-ի համար:
- Փոխարինեք y-ը f−1(x) f − 1 (x)-ով:
- Ստուգեք ձեր աշխատանքը՝ ստուգելով, որ (f∘f−1)(x)=x (f ∘ f − 1) (x) = x և (f−1∘f)(x)=x (f − 1 ∘ f) (x) = x երկուսն էլ ճշմարիտ են:
ինչ է հակադարձ ֆունկցիայի օրինակը: Հակադարձ գործառույթներ , ամենաընդհանուր իմաստով են գործառույթները որոնք «հակադարձում» են միմյանց։ Համար օրինակ , եթե f-ը a-ն տանում է b, ապա the հակադարձ , f − 1 f^{-1} f−1f, սկիզբ վերնագիր, մինուս, 1, վերջի վերնագիր, պետք է b-ից a տանի:
Այստեղ ինչպե՞ս եք տարբերում հակադարձ ֆունկցիաները:
Հակադարձ եռանկյունաչափական ֆունկցիաների ածանցյալներ
- Օգտագործե՛ք հակադարձ ֆունկցիայի թեորեմը՝ գտնելու g(x)=sin−1x-ի ածանցյալը:
- Քանի որ x-ի համար [−π2, π2] միջակայքում, f(x)=sinx-ը g(x)=sin−1x-ի հակադարձն է, սկսեք գտնելով f′(x):
- f′(x)=cosx.
- f′(g(x))=cos(sin−1x)=√1−x2.
- g′(x)=ddx(sin−1x)=1f′(g(x))=1√1−x2.
Ի՞նչ է ինքնահակադարձ ֆունկցիան:
Ա ինքնահակադարձ ֆունկցիա է ֆունկցիան f, այնպիսին, որ y=f(x), հատուկ հատկությամբ, որ ff(x)=x, կամ գրված է այլ կերպ, f(x)=f−1(x)
Խորհուրդ ենք տալիս:
Արդյո՞ք խորանարդ ֆունկցիան ունի հակադարձ:
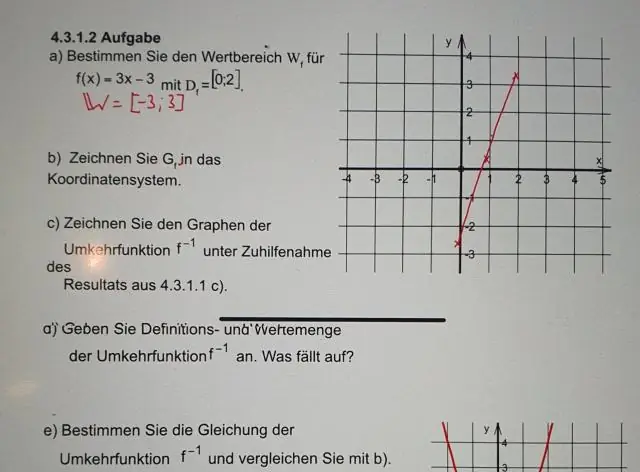
ԸՆԴՀԱՆՈՒՐ, ՀԱԿԱՌՈՂ ՉՈՒՆԻ, ԵԹԵ ՄԵԿ-ՄԵԿ ՖՈՒՆԿՑԻԱ ՉԷ, քանի որ միայն այդպիսի ֆունկցիաներն են շրջելի: ? ԲԱՅՑ եթե խորանարդ ֆունկցիան ունի հետևյալ ձևը/կարող է փոխարկվել հետևյալ ձևի, այն շրջելի է՝ (i) f(x)=(ax+b)³+c, a≠0, b,c∈|R , իր բնական տիրույթով՝ x∈|R կամ կրճատված տիրույթով
Ի՞նչ է անընդհատ ֆունկցիան հաշվարկում:
Եթե ֆունկցիան շարունակական է ցանկացած արժեքի դեպքում, ապա մենք ասում ենք, որ ֆունկցիան շարունակական է այդ միջակայքում: Եվ եթե ֆունկցիան շարունակական է ցանկացած միջակայքում, ապա մենք այն պարզապես անվանում ենք շարունակական ֆունկցիա։ Հաշվարկը, ըստ էության, կապված է ֆունկցիաների հետ, որոնք շարունակական են իրենց տիրույթների յուրաքանչյուր արժեքով
Ի՞նչ է հակադարձ համամասնությունը և օրինակները:

Հակադարձ համամասնություն. Հակադարձ համամասնությունը տեղի է ունենում, երբ մի արժեքը մեծանում է, իսկ մյուսը նվազում է: Օրինակ, աշխատանքում ավելի շատ աշխատողներ կնվազեցնեն առաջադրանքն ավարտելու ժամանակը: Դրանք հակադարձ համեմատական են
Ի՞նչ է կոմպոզիտային ֆունկցիան հաշվարկում:

Նման երկու (կամ ավելի) ֆունկցիաների համակցումը կոչվում է ֆունկցիաների կոմպոզիցիա, իսկ ստացված ֆունկցիան կոչվում է կոմպոզիտային ֆունկցիա: Կոմպոզիտային ֆունկցիայի կանոնը ցույց է տալիս մեզ ավելի արագ ճանապարհ: Կանոն 7 (Կոմպոզիտային ֆունկցիայի կանոն (նաև հայտնի է որպես շղթայի կանոն)) Եթե f(x) = h(g(x)), ապա f (x) = h (g(x)) × g (x)
Ո՞րն է հակադարձ հիպերբոլիկ սինուսի ֆունկցիան:

Հիպերբոլիկ սինուս ֆունկցիան՝ sinhx, մեկ առ մեկ է, և հետևաբար ունի լավ սահմանված հակադարձ՝ sinh−1x, որը ցույց է տրված նկարում կապույտով: Պայմանականորեն cosh−1x-ը վերցվում է որպես դրական y թիվ այնպես, որ x=coshy
