
Բովանդակություն:
- Հեղինակ Miles Stephen [email protected].
- Public 2024-01-18 08:16.
- Վերջին փոփոխված 2025-01-22 17:00.
Կետային արտադրյալը կատարում է հետևյալ հատկությունները, եթե a, b և c-ն իրական վեկտորներ են, իսկ r-ը սկալյար է։
- Փոխադրական. որը բխում է սահմանումից (θ-ը a-ի և b-ի միջև եղած անկյունն է).
- Վեկտորի վրա բաշխված գումարում.
- Երկգծային:
- Սկալյար բազմապատկում:
Հետագայում կարելի է նաև հարցնել՝ որո՞նք են կետային արտադրանքի 4 հատկությունները։
Dot Product-ի հատկությունները
- u · v = |u||v| cos θ
- u · v = v · u.
- u · v = 0, երբ u-ը և v-ն ուղղանկյուն են:
- 0 · 0 = 0.
- |վ|2 = v · v.
- a (u·v) = (a u) · v.
- (au + bv) · w = (au) · w + (bv) · w.
Կարելի է նաև հարցնել՝ ի՞նչ հատկություններ ունի խաչաձև արտադրանքը։ Խաչի արտադրանքի հատկությունները.
- Երկու վեկտորների խաչաձեւ արտադրյալի երկարությունն է.
- Երկու վեկտորների խաչաձև արտադրյալի երկարությունը հավասար է երկու վեկտորներով որոշված զուգահեռագծի մակերեսին (տես ստորև նկարը):
- Anticommutativity:
- Բազմապատկում սկալյարներով.
- Բաշխվածություն:
Նմանապես, դուք կարող եք հարցնել, թե ինչ է նշանակում կետային արտադրանք:
Ա կետային արտադրանք է սկալյար արժեւորել դա է նույն թվով բաղադրիչներով երկու վեկտորների գործողության արդյունք: Հաշվի առնելով երկու A և B վեկտորները՝ յուրաքանչյուրը n բաղադրիչով, the կետային արտադրանք հաշվարկվում է այսպես՝ A · B = A1Բ1 + + Ա Բ . Այն կետային արտադրանք Այսպիսով, գումարն է ապրանքներ երկու վեկտորների յուրաքանչյուր բաղադրիչից:
Որո՞նք են վեկտորների հատկությունները:
Վեկտորների հանրահաշվական հատկությունները
- Կոմուտատիվ (վեկտոր) P + Q = Q + P.
- Ասոցիատիվ (վեկտոր) (P + Q) + R = P + (Q + R)
- Հավելվածի ինքնությունը Կա վեկտոր 0 այդպիսին:
- Հակադարձ հավելում ցանկացած P-ի համար կա այնպիսի վեկտոր -P, որ P + (-P) = 0:
- Բաշխիչ (վեկտոր) r(P + Q) = rP + rQ:
- Բաշխիչ (սկալար) (r + s) P = rP + sP.
- Ասոցիատիվ (սկալար) r(sP) = (rs)P.
Խորհուրդ ենք տալիս:
Որո՞նք են կետային մուտացիաների երկու տեսակները:

Կետային մուտացիաների երկու տեսակ կա՝ անցումային մուտացիաներ և տրանսվերսիոն մուտացիաներ։ Անցումային մուտացիաները տեղի են ունենում, երբ պիրիմիդինային բազան (այսինքն՝ թիմին [T] կամ ցիտոսին [C]) փոխարինում է մեկ այլ պիրիմիդինային բազայի կամ երբ պուրինային բազան (այսինքն՝ ադենինը [A] կամ գուանինը [G]) փոխարինում է մեկ այլ պուրինային բազայի։
Ինչպե՞ս եք հաշվարկում Pearson արտադրանքի պահերի հարաբերակցությունը SPSS-ում:
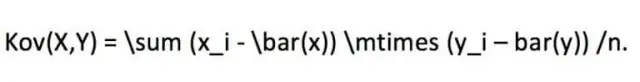
Երկփոփոխական Pearson հարաբերակցությունը գործարկելու համար սեղմեք Վերլուծել > Հարաբերակցել > Երկփոփոխություն: Ընտրեք Height և Weight փոփոխականները և տեղափոխեք դրանք Փոփոխականներ տուփ: Հարաբերակցության գործակիցների տարածքում ընտրեք Pearson: Նշանակության թեստում ընտրեք ձեր ուզած նշանակության թեստը՝ երկպոչ կամ միապոչ
Ինչպե՞ս եք օգտագործում աջ ձեռքի կանոնը խաչաձև արտադրանքի համար:
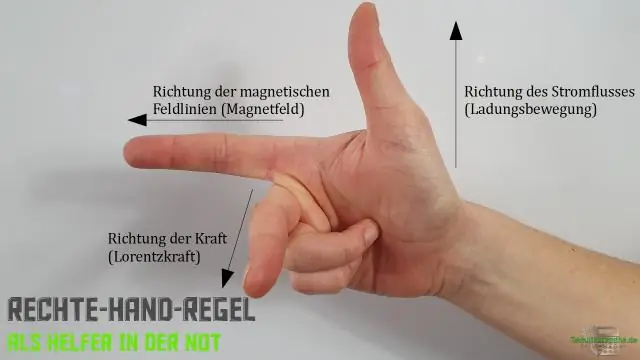
Աջ ձեռքի կանոնը սահմանում է, որ վեկտորների խաչաձև արտադրյալի կողմնորոշումը որոշվում է՝ դնելով և պոչից պոչը՝ հարթեցնելով աջ ձեռքը, երկարացնելով այն դեպի ուղղությամբ և այնուհետև ոլորելով մատները այն ուղղությամբ, որով կազմում է անկյունը: Բութ մատն այնուհետև ուղղված է դեպի
Որո՞նք են գագաթները կետային սյուժեի վրա:

Գագաթներ և տարածում Որոշեք գագաթները, որոնք ամենաշատ կետերն ունեցող աղբամաններն են: Գագաթները ներկայացնում են նմուշի ամենատարածված արժեքները: Գնահատեք ձեր ընտրանքի տարածվածությունը՝ հասկանալու համար, թե որքանով են տարբերվում ձեր տվյալները: Օրինակ, հաճախորդի սպասման ժամանակների այս կետային պլանում տվյալների գագաթնակետը տեղի է ունենում մոտ 6 րոպեում
Որո՞նք են կյանքի երեք ոլորտները և որո՞նք են դրանց յուրահատուկ հատկությունները:
Երեք տիրույթները ներառում են. Archaea - ամենահին հայտնի տիրույթը, բակտերիաների հնագույն ձևերը: Բակտերիաներ - բոլոր մյուս բակտերիաները, որոնք ներառված չեն Archaea տիրույթում: Էուկարիա - բոլոր այն օրգանիզմները, որոնք էուկարիոտ են կամ պարունակում են թաղանթով կապված օրգանելներ և միջուկներ
