
- Հեղինակ Miles Stephen [email protected].
- Public 2023-12-15 23:37.
- Վերջին փոփոխված 2025-01-22 17:00.
Գծային ռեգրեսիա օգտագործվում է Y շարունակական փոփոխականի արժեքը կանխատեսելու համար՝ հիմնված մեկ կամ մի քանի մուտքային կանխատեսող X փոփոխականների վրա: Նպատակն է մաթեմատիկական բանաձև հաստատել պատասխան փոփոխականի (Y) և կանխատեսող փոփոխականների (Xs) միջև: Դուք կարող եք օգտագործել այս բանաձևը Y-ը կանխատեսելու համար, երբ հայտնի են միայն X արժեքները:
Նմանապես, ի՞նչ է ռեգրեսիան R ծրագրավորման մեջ:
Ռ - Գծային Հետընթաց . Գովազդներ. Հետընթաց վերլուծությունը շատ լայնորեն օգտագործվող վիճակագրական գործիք է երկու փոփոխականների միջև հարաբերությունների մոդել ստեղծելու համար: Այս փոփոխականներից մեկը կոչվում է կանխատեսող փոփոխական, որի արժեքը հավաքվում է փորձերի միջոցով:
Բացի վերևից, ո՞րն է լավ R քառակուսի արժեքը: Ռ - քառակուսի միշտ գտնվում է 0-ից 100%-ի միջև. 0%-ը ցույց է տալիս, որ մոդելը չի բացատրում պատասխանի տվյալների փոփոխականությունը իր միջինի շուրջ: 100% ցույց է տալիս, որ մոդելը բացատրում է պատասխանի տվյալների ողջ փոփոխականությունը իր միջինի շուրջ:
Այս կերպ, ո՞րն է լավ R քառակուսի արժեքը գծային ռեգրեսիայի համար:
Նույն տվյալների հավաքածուի համար՝ ավելի բարձր Ռ - քառակուսի արժեքներ ներկայացնում են ավելի փոքր տարբերություններ դիտարկված տվյալների և հարմարեցվածների միջև արժեքներ . Ռ - քառակուսի կախված փոփոխական փոփոխության տոկոսն է, որը a գծային մոդելը բացատրում է. Ռ - քառակուսի միշտ 0-ից 100% է.
Ինչպե՞ս եք մուտքագրում տվյալները R-ում:
Դու կարող ես մուտքագրել տվյալներ պարզապես մուտքագրելով արժեքներ և սեղմելով վերադարձ կամ ներդիր: Նաև կարող եք օգտագործել վեր և վար սլաքները նավարկելու համար: Ավարտելուց հետո պարզապես ընտրեք Ֆայլ > Փակել: Եթե մուտքագրեք ls(), այժմ պետք է տեսնեք ձեր ստեղծած փոփոխականների անունները:
Խորհուրդ ենք տալիս:
Ինչպե՞ս եք հաշվարկում ոչ գծային ռեգրեսիան:

Եթե ձեր մոդելը օգտագործում է հավասարում Y = a0 + b1X1 ձևով, ապա դա գծային ռեգրեսիոն մոդել է: Եթե ոչ, ապա դա ոչ գծային է: Y = f(X,β) + ε X = p կանխատեսողների վեկտոր, β = k պարամետրերի վեկտոր, f(-) = հայտնի ռեգրեսիոն ֆունկցիա, ε = սխալի տերմին
Որո՞նք են գծային ծրագրավորման ենթադրությունները:

Գծային ծրագրավորման որոշակիության պայմանների ենթադրություններ. Դա նշանակում է, որ օբյեկտի և սահմանափակումների թվերը հայտնի են որոշակիորեն և փոփոխվում են ուսումնասիրվող ժամանակահատվածում: Գծայինություն կամ համաչափություն. Լրացուցիչ. Բաժանելիություն. Ոչ բացասական փոփոխական: Վերջնականություն. Օպտիմալություն
Ո՞րն է գծային ծրագրավորման սիմպլեքս մեթոդը:
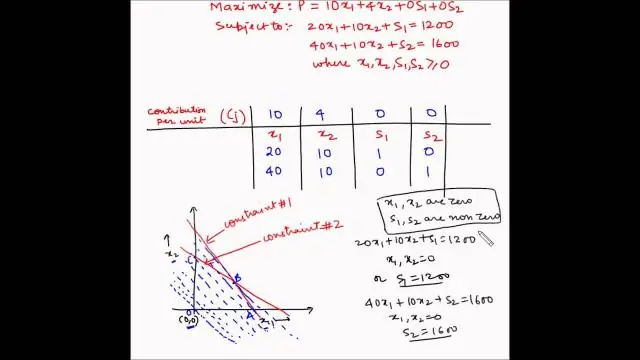
Սիմպլեքս մեթոդ. Սիմպլեքս մեթոդ, ստանդարտ տեխնիկա գծային ծրագրավորման մեջ օպտիմալացման խնդիր լուծելու համար, որը սովորաբար ներառում է ֆունկցիա և մի քանի սահմանափակումներ, որոնք արտահայտվում են որպես անհավասարություններ: Անհավասարությունները սահմանում են բազմանկյուն շրջան (տես բազմանկյուն), և լուծումը սովորաբար գտնվում է գագաթներից մեկում
Ինչպե՞ս եք լուծում գծային ծրագրավորման խնդիրը անկյունների մեթոդով:
ԱՆԿՅՈՒՆՆԵՐԻ ՄԵԹՈԴ Գծե՛ք իրականանալի բազմությունը (տարածաշրջան), S. Գտե՛ք S-ի բոլոր գագաթների (անկյունային կետերի) Ճշգրիտ կոորդինատները: Գնահատե՛ք P-ի նպատակային ֆունկցիան յուրաքանչյուր գագաթում: Առավելագույնը (եթե այն գոյություն ունի) ամենամեծ արժեքն է: P մի գագաթի վրա: Նվազագույնը P-ի ամենափոքր արժեքն է գագաթի վրա
Ինչի համար է օգտագործվում ոչ գծային ռեգրեսիան:

Ոչ գծային ռեգրեսիան ռեգրեսիոն վերլուծության ձև է, որտեղ տվյալները համապատասխանում են մոդելին և այնուհետև արտահայտվում են որպես մաթեմատիկական ֆունկցիա: Ոչ գծային ռեգրեսիան օգտագործում է լոգարիթմական ֆունկցիաներ, եռանկյունաչափական ֆունկցիաներ, էքսպոնենցիալ ֆունկցիաներ, հզորության ֆունկցիաներ, Լորենցի կորեր, Գաուսի ֆունկցիաներ և հարմարեցման այլ մեթոդներ։
