Video: Ի՞նչ է ապոտեմը երկրաչափության մեջ:
2024 Հեղինակ: Miles Stephen | [email protected]. Վերջին փոփոխված: 2023-12-15 23:37
Այն ապոտեմ Կանոնավոր բազմանկյունի (երբեմն կրճատ՝ ապո) գծային հատվածն է կենտրոնից մինչև նրա կողմերից մեկի միջնակետը։ Համարժեքորեն դա այն ուղիղն է, որը գծված է բազմանկյան կենտրոնից, որը ուղղահայաց է նրա կողմերից մեկին: Բառը ապոտեմ «կարող է վերաբերել նաև այդ գծի հատվածի երկարությանը։
Ինչ վերաբերում է դրան, ի՞նչ է նշանակում Ապոթեմը երկրաչափության մեջ:
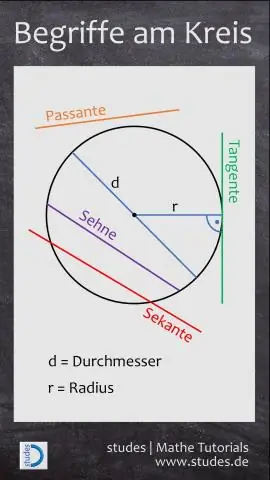
Ապաթեմ . ավելին Կանոնավոր բազմանկյունի կենտրոնից մինչև կողմի միջնակետ հեռավորությունը: (Շրջանակի համար այն է հեռավորությունը կենտրոնից մինչև ակորդի միջնակետը։) Կանոնավոր բազմանկյուններ – Հատկություններ։
Նաև գիտեք, թե որն է կանոնավոր հնգանկյունի ապոթեմը: Այն ապոտեմ գիծն է կենտրոնից հնգանկյուն դեպի մի կողմ՝ հատելով կողմը 90º ուղիղ անկյան տակ: Մի շփոթեք ապոտեմ շառավղով, որը միջին կետի փոխարեն դիպչում է անկյունին (գագաթին):
Հետևաբար, ինչպե՞ս եք գտնում կանոնավոր բազմանկյան ապոտեմը:
Կարող ենք օգտվել նաև տարածքից բանաձեւը դեպի գտիր ապոտեմը եթե գիտենք a-ի և՛ մակերեսը, և՛ պարագիծը բազմանկյուն . Դա պայմանավորված է նրանով, որ մենք կարող ենք լուծել a in the բանաձեւը , A = (1/2)aP, երկու կողմերը բազմապատկելով 2-ով և բաժանելով P-ի վրա՝ ստանալով 2A / P = a: Այստեղ, որ ապոտեմ ունի 4,817 միավոր երկարություն։
Ինչպե՞ս գտնել եռանկյան մակերեսը:
Դեպի գտնել որ տարածք ա եռանկյուն , հիմքը բազմապատկեք բարձրությամբ, այնուհետև բաժանեք 2-ի։ 2-ի բաժանումը գալիս է նրանից, որ զուգահեռագիծը կարելի է բաժանել 2-ի։ եռանկյուններ . Օրինակ, ձախ կողմում գտնվող գծապատկերում նշված է տարածք յուրաքանչյուրից եռանկյուն հավասար է կեսի տարածք զուգահեռագծից։
Խորհուրդ ենք տալիս:
Ի՞նչ է արտացոլման գիծը երկրաչափության մեջ:
Արտացոլման գիծ. • մի գիծ ինչ-որ բանի միջև, որը կոչվում է նախապատկեր և դրա հայելային արտացոլումը
Ինչպե՞ս եք գտնում Preimage-ը երկրաչափության մեջ:
T(V) պատկերը սահմանվում է որպես բազմություն {k | k=T(v) որոշ v-ի համար V}-ում: Այսպիսով, x=T(y) որտեղ y-ը T^-1(S) տարրն է: S-ի նախապատկերը բազմությունն է {m | T(m)-ը S}-ում է: Այսպիսով, T(y)-ը S-ում է, ուստի քանի որ x=T(y), մենք ունենք, որ x-ը S-ում է
Որո՞նք են ամուր թվերը երկրաչափության մեջ:
Պինդ ֆիգուրները եռաչափ ֆիգուրներ են, որոնք ունեն երկարություն, լայնություն և բարձրություն: Տե՛ս ստորև եռաչափ պատկերների մի քանի օրինակ: Պրիզման պոլիէդրոն է՝ ուղիղ երկու դեմքերով, որոնք համահունչ են և զուգահեռ: Այս դեմքերը կոչվում են հիմքեր: Մյուս դեմքերը կոչվում են կողային դեմքեր
Դուք սովորում եք եռանկյունաչափությունը երկրաչափության մեջ:
Նախքան եռանկյունաչափություն սովորելը պետք է արդեն ծանոթ լինեք հանրահաշիվին և երկրաչափությանը: Հանրահաշվից դուք պետք է հարմար լինեք հանրահաշվական արտահայտությունների մանիպուլյացիայի և հավասարումների լուծմանը: Երկրաչափությունից դուք պետք է իմանաք նմանատիպ եռանկյունների, Պյութագորասի թեորեմի և մի քանի այլ բաների մասին, բայց ոչ շատ
Քանի՞ թեորեմ և պոստուլատ կա երկրաչափության մեջ:
Պոստուլատը պնդում է, որը ենթադրվում է ճիշտ առանց ապացույցների: Թեորեմը ճշմարիտ պնդում է, որը կարելի է ապացուցել: Ստորև թվարկված են վեց պոստուլատներ և այն թեորեմները, որոնք կարելի է ապացուցել այս պոստուլատներից