Video: Ինչու են ռացիոնալ գործառույթները սահմանափակումներ:
2024 Հեղինակ: Miles Stephen | [email protected]. Վերջին փոփոխված: 2023-12-15 23:37
Դոմեն սահմանափակումներ ա ռացիոնալ գործառույթ կարելի է որոշել՝ զրոյի հավասարեցնելով հայտարարը և լուծելով. x-արժեքները, որոնց հայտարարը հավասար է զրոյի են կոչվում են եզակիություններ և են ոչ տիրույթում ֆունկցիան.
Նմանապես, ինչու են ռացիոնալ գործառույթները կարևոր:
Նշանակություն. « Ռացիոնալ ֆունկցիա «այսպես է կոչվում ա ֆունկցիան որը կարող է ներկայացվել որպես բազմանդամների քանորդ, ճիշտ ինչպես ա ռացիոնալ թիվն այն թիվն է, որը կարող է արտահայտվել որպես ամբողջ թվերի քանորդ: Ռացիոնալ գործառույթներ մատակարարում կարևոր օրինակներ և բնականաբար տեղի են ունենում բազմաթիվ համատեքստերում:
Նմանապես, ռացիոնալ ֆունկցիաներն ունե՞ն շրջադարձային կետեր: 4 Ամփոփում. n աստիճանի բազմանդամ ունի առավելագույնը n իրական զրո և n−1 շրջադարձային կետեր . Ա ռացիոնալ գործառույթ է ֆունկցիան f(x)=P(x)Q(x), f (x) = P (x) Q (x), որտեղ P(x) և Q(x) են երկու բազմանդամները.
Նաև հարց է, թե ինչ է ռացիոնալ ֆունկցիայի օրինակը:
Օրինակներ -ից Ռացիոնալ գործառույթներ Այն ֆունկցիան R(x) = (x^2 + 4x - 1) / (3x^2 - 9x + 2) է ռացիոնալ գործառույթ քանի որ x^2 + 4x - 1 համարիչը բազմանդամ է, իսկ հայտարարը 3x^2 - 9x + 2 նույնպես բազմանդամ է։
Որո՞նք են ռացիոնալ ֆունկցիաների առանձնահատկությունները:
Երկու կարևոր Հատկություններ ցանկացածից ռացիոնալ գործառույթ r(x)=p(x)q(x) r (x) = p (x) q (x) ցանկացած զրո և ուղղահայաց ասիմպտոտներ են. ֆունկցիան կարող է ունենալ. Այս ասպեկտները Ա ռացիոնալ գործառույթ սերտորեն կապված են այնտեղ, որտեղ համարիչը և հայտարարը, համապատասխանաբար, զրո են:
Խորհուրդ ենք տալիս:
Ամբողջ թվերը միշտ ռացիոնալ թվե՞ն են, թե՞ երբեք:
1.5-ը ռացիոնալ թիվ է, որը կարելի է գրել այսպես՝ 3/2, որտեղ 3-ը և 2-ը երկուսն էլ ամբողջ թվեր են: Այստեղ ռացիոնալ 8 թիվը ամբողջ թիվ է, բայց 1,5 ռացիոնալ թիվը ամբողջ թիվ չէ, քանի որ 1,5-ը ամբողջ թիվ չէ։ Այսպիսով, մենք կարող ենք ասել, որ ռացիոնալ թիվը ամբողջ թիվ է երբեմն ոչ միշտ: Հետևաբար, երբեմն ճիշտ պատասխանն է
Ինչպե՞ս եք գտնում չսահմանված արժեքներ ռացիոնալ արտահայտություններում:
Ռացիոնալ արտահայտությունն անորոշ է, երբ հայտարարը հավասար է զրոյի: Ռացիոնալ արտահայտությունը անորոշ դարձնող արժեքները գտնելու համար հայտարարը հավասարեցրեք զրոյի և լուծեք ստացված հավասարումը: Օրինակ՝ 0 7 2 3 x x &մինուս; Չսահմանված է, քանի որ զրոն հայտարարի մեջ է
Ի՞նչ է ասում ռացիոնալ արմատի թեորեմը:
Ռացիոնալ արմատի թեորեմ. Թեորեմն ասում է, որ յուրաքանչյուր ռացիոնալ լուծում x = p/q, գրված ամենացածր թվերով այնպես, որ p և q համեմատաբար պարզ լինեն, բավարարում է. p-ն a0 հաստատուն անդամի ամբողջ թվային գործակիցն է, և
Ինչու՞ ենք սահմանում սահմանափակումներ ռացիոնալ արտահայտման համար և ե՞րբ ենք նշում սահմանափակումները։
Մենք նշում ենք սահմանափակումներ, քանի որ դա կարող է հանգեցնել x-ի որոշ արժեքներում հավասարման չսահմանված լինելուն: Ռացիոնալ արտահայտությունների ամենատարածված սահմանափակումը N/0-ն է: Սա նշանակում է, որ ցանկացած թիվ, որը բաժանված է զրոյի, անորոշ է: Օրինակ, f(x) = 6/x² ֆունկցիայի համար, երբ փոխարինում եք x=0-ին, կստացվի 6/0, որն անորոշ է:
Ինչպե՞ս կարող եմ կիրառել չափերի սահմանափակումներ AutoCAD-ում:
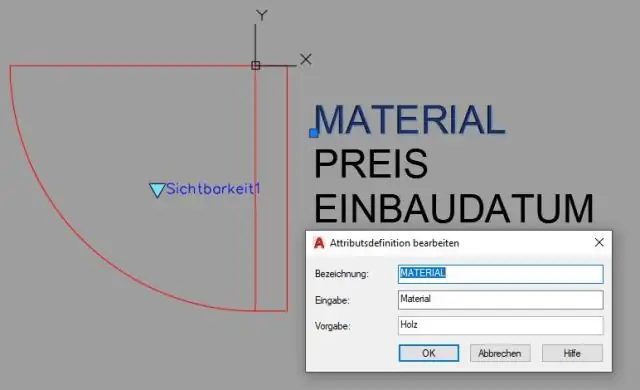
Այս քայլերը ներկայացնում են ծավալային սահմանափակումների պարզ օրինակ. Սկսեք նոր գծագիր և ընթացիկ դարձրեք ժապավենի պարամետրային ներդիրը: Միացրեք համապատասխան ճշգրիտ նկարչական օժանդակ սարքերը կարգավիճակի տողում, ինչպիսիք են Snap, Ortho և Osnap: Գծե՛ք բավականին ճշգրիտ երկրաչափություն՝ կիրառելով ճշգրիտ տեխնիկա