- Հեղինակ Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:37.
- Վերջին փոփոխված 2025-06-01 05:04.
Լոգարիթմական ֆունկցիաներ -ի հակադարձներն են էքսպոնենցիալ ֆունկցիաներ . -ի հակադարձը էքսպոնենցիալ ֆունկցիա y = աx է x = ay. Այն լոգարիթմական ֆունկցիա y = գրանցամատյանաx-ը սահմանվում է որպես համարժեք էքսպոնենցիալ հավասարում x = ay. y = գրանցամատյանաx միայն հետևյալ պայմաններով. x = ay, a > 0 և a≠1.
Համապատասխանաբար, ո՞րն է տարբերությունը էքսպոնենցիալ և լոգարիթմական ֆունկցիաների միջև:
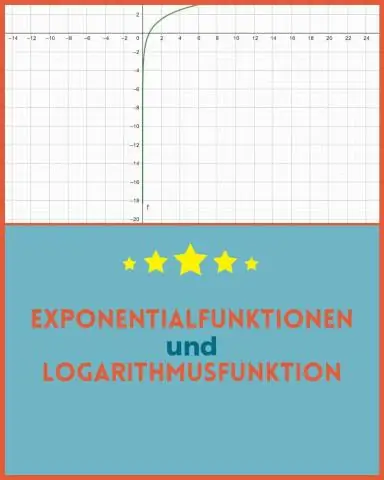
ան-ի հակադարձը էքսպոնենցիալ ֆունկցիա է լոգարիթմական ֆունկցիա իսկ հակադարձ ա լոգարիթմական ֆունկցիա է էքսպոնենցիալ ֆունկցիա . Ուշադրություն դարձրեք նաև գրաֆիկի վրա, որ քանի որ x-ն ավելի ու ավելի է մեծանում, ֆունկցիան f(x) արժեքն ավելի ու ավելի կտրուկ աճում է:
ո՞րն է լոգարիթմական ֆունկցիայի օրինակը: Ա լոգարիթմ ցուցիչ է։ Ցանկացած էքսպոնենցիալ արտահայտություն կարող է վերագրվել լոգարիթմական ձեւը։ Համար օրինակ , եթե ունենք 8 = 23, ապա հիմքը 2 է, ցուցիչը՝ 3, իսկ արդյունքը՝ 8։ Սա կարելի է վերագրել. լոգարիթմական ձևը որպես. 3 = գերան 2 8.
Ինչ վերաբերում է դրան, ի՞նչ է էքսպոնենցիալ լոգարիթմը:
Ըստ սահմանման. գերան բy = x նշանակում է b x = y. Համապատասխան յուրաքանչյուր լոգարիթմ b հիմքով ֆունկցիա, տեսնում ենք, որ կա an էքսպոնենցիալ ֆունկցիա b հիմքով. y = b x. Ան էքսպոնենցիալ ֆունկցիան ա-ի հակառակն է լոգարիթմ ֆունկցիան։
Ո՞րն է էքսպոնենցիալ ֆունկցիայի օրինակ:
Ան-ում էքսպոնենցիալ ֆունկցիա , անկախ փոփոխականը կամ x-արժեքն է ցուցիչ , մինչդեռ հիմքը հաստատուն է։ Համար օրինակ , y = 2x կլինի an էքսպոնենցիալ ֆունկցիա . Ահա թե ինչ տեսք ունի. Բանաձևը ան էքսպոնենցիալ ֆունկցիա y = abx է, որտեղ a և b հաստատուններ են:
Խորհուրդ ենք տալիս:
Ինչպե՞ս գտնել լոգարիթմական հավասարման ասիմպտոտը:

Հիմնական կետերը Երբ գծագրվում է, լոգարիթմական ֆունկցիան իր ձևով նման է քառակուսի արմատի ֆունկցիային, բայց ունի ուղղահայաց ասիմպտոտ, երբ x-ը աջից մոտենում է 0-ին: (1,0) կետը y=logbx y = l o g b x ձևի բոլոր լոգարիթմական ֆունկցիաների գրաֆիկի վրա է, որտեղ b դրական իրական թիվ է։
Ի՞նչ է նշանակում խտացնել լոգարիթմական արտահայտությունը:

Լոգարիթմական արտահայտությունը լոգարիթմներ ունեցող արտահայտություն է: Լոգարիթմական արտահայտությունները խտացնելը նշանակում է օգտագործել լոգարիթմի օրենքները՝ լոգարիթմի արտահայտությունները ընդլայնված ձևից խտացված ձևի իջեցնելու համար: Լոգարիթմի օրենքների/հատկությունների իմացությունը կարևոր կլինի լոգարիթմի արտահայտությունների խտացման համար
Ինչպե՞ս եք պատկերացնում լոգարիթմական ֆունկցիաները հաշվիչի վրա:

Գրաֆիկական հաշվիչի վրա հիմքը e լոգարիթմը ln բանալին է: Երեքն էլ նույնն են։ Եթե ունեք logBASE ֆունկցիա, այն կարող է օգտագործվել ֆունկցիա մուտքագրելու համար (տես ստորև Y1-ում): Եթե ոչ, օգտագործեք Change of Base բանաձևը (տե՛ս ստորև Y2-ում)
Ի՞նչ է տեղի ունենում լոգարիթմական փուլում:

Բակտերիաների աճի կորը Այնուհետև պոպուլյացիան մտնում է լոգարիթմական փուլ, որտեղ բջիջների թիվը մեծանում է լոգարիթմական ձևով, և յուրաքանչյուր բջիջների սերունդ տեղի է ունենում նույն ժամանակային ընդմիջումով, ինչ նախորդները, ինչը հանգեցնում է յուրաքանչյուր բջիջի բաղադրիչների հավասարակշռված աճի:
Ինչպե՞ս եք պատկերացնում լոգարիթմական ֆունկցիաները:

Լոգարիթմական ֆունկցիաների գրաֆիկական ձևավորում Ցանկացած ֆունկցիայի հակադարձ ֆունկցիայի գրաֆիկը y=x տողի շուրջ ֆունկցիայի գրաֆիկի արտացոլումն է։ Լոգարիթմական ֆունկցիան՝ y=logb(x), կարելի է տեղափոխել k միավոր ուղղահայաց, իսկ h միավոր՝ հորիզոնական՝ y=logb(x+h)+k հավասարմամբ։ Դիտարկենք y=[log2(x+1)−3 լոգարիթմական ֆունկցիան:
