Video: Ի՞նչ է զուգահեռ ֆունկցիան:
2024 Հեղինակ: Miles Stephen | [email protected]. Վերջին փոփոխված: 2023-12-15 23:37
Օրինակ՝ նույնականացում Զուգահեռ և ուղղահայաց գծեր
Զուգահեռ գծերն ունեն նույն թեքությունը։ Քանի որ գործառույթները f(x)=2x+3 f (x) = 2 x + 3 և j(x)=2x−6 j (x) = 2 x − 6 յուրաքանչյուրն ունի 2 թեքություն, դրանք ներկայացնում են. զուգահեռ տողեր. Ուղղահայաց գծերն ունեն բացասական փոխադարձ թեքություններ
Նմանապես, ո՞րն է զուգահեռ ուղիղների իմաստը:
Զուգահեռ գծեր երկուսն են տողեր որոնք միշտ նույն հեռավորության վրա են միմյանցից և երբեք չեն շոշափում: Երկուսի համար տողեր լինել զուգահեռ , դրանք պետք է գծված լինեն նույն հարթության վրա՝ պատի կամ թղթի նման կատարյալ հարթ մակերեսով։ Ցանկացած տող որն ունի նույն թեքությունը, ինչ բնօրինակը, երբեք չի հատվի դրա հետ:
Հետագայում հարցն այն է, թե ինչպես եք իմանում, որ երկու ուղիղները զուգահեռ են: Տեսնել արդյոք կամ ոչ երկու ուղիղները զուգահեռ են , պետք է համեմատել դրանց թեքությունները։ Երկու ուղիղները զուգահեռ են, եթե և միայն եթե նրանց թեքությունները հավասար են: 2x – 3y = 4 տողը ստանդարտ ձևով է: Ընդհանուր առմամբ, Ax + By = C ձևով տողը ունի –A/B թեքություն; հետևաբար, q ուղիղի թեքությունը պետք է լինի. 2 /–3 = 2 /3.
Հետագայում հարցն այն է, թե որն է տարբերությունը ուղղահայաց և զուգահեռ:
Երկու տող ասվում է զուգահեռ երբ դրանք միմյանցից հավասար են և երբեք չեն հատվի կամ դիպչի: Պարզ ասած՝ երկուսի թեքությունը զուգահեռ տողերը հավասար են. -ի թեքություն ուղղահայաց գծերը, մյուս կողմից, միմյանց բացասական փոխադարձներ են, ինչը նշանակում է, որ գծերը հատվում են միմյանց ուղիղ անկյան տակ:
Ո՞րն է զուգահեռի նշանը:
Երկու ուղիղները, երկուսն էլ նույն հարթության մեջ, որոնք երբեք չեն հատվում, կոչվում են զուգահեռ տողեր. Զուգահեռ գծերը միշտ մնում են միմյանցից նույն հեռավորության վրա: Այն խորհրդանիշ // օգտագործվում է նշելու համար զուգահեռ տողեր.
Խորհուրդ ենք տալիս:
Ինչպե՞ս որոշել, արդյոք ֆունկցիան ունի հորիզոնական շոշափող գիծ:
Հորիզոնական գծերը ունեն զրոյական թեքություն: Հետևաբար, երբ ածանցյալը զրո է, շոշափող գիծը հորիզոնական է: Հորիզոնական շոշափող գծերը գտնելու համար օգտագործեք ֆունկցիայի ածանցյալը՝ զրոները գտնելու և դրանք նորից միացնելու սկզբնական հավասարման մեջ։
Ինչպե՞ս գծագրել հիպերբոլիկ ֆունկցիան:
Հիպերբոլիկ ֆունկցիաների գրաֆիկները sinh(x) = (e x - e -x)/2. cosh(x) = (e x + e -x)/2. tanh(x) = sinh(x) / cosh(x) = (ex - e -x) / (ex + e -x) coth(x) = cosh(x) / sinh(x) = (ex + e - x) / (ex - e -x) sech (x) = 1 / cosh (x) = 2 / (ex + e -x) csch (x) = 1 / sinh (x) = 2 / (նախկին - e - x)
Ֆունկցիան գծային է, թե ոչ գծային:
Գծային ֆունկցիան y = mx + b ստանդարտ ձևով ֆունկցիա է, որտեղ m-ը թեքությունն է, իսկ b-ը՝ y-հատվածը, և որի գրաֆիկը նման է ուղիղ գծի: Կան այլ գործառույթներ, որոնց գրաֆիկը ուղիղ գիծ չէ: Այս ֆունկցիաները հայտնի են որպես ոչ գծային ֆունկցիաներ և դրանք լինում են տարբեր ձևերով
Արդյո՞ք խորանարդ ֆունկցիան ունի հակադարձ:
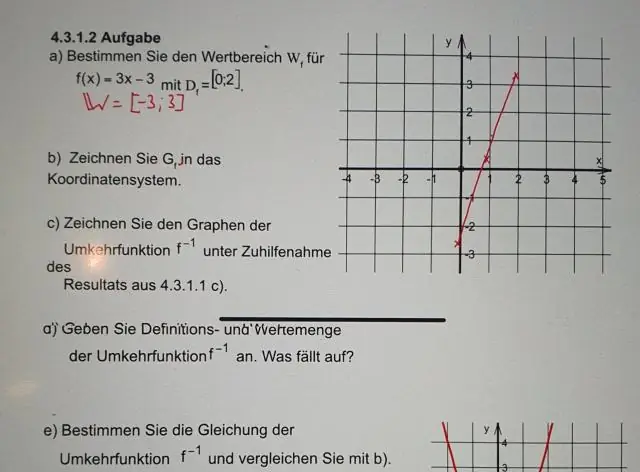
ԸՆԴՀԱՆՈՒՐ, ՀԱԿԱՌՈՂ ՉՈՒՆԻ, ԵԹԵ ՄԵԿ-ՄԵԿ ՖՈՒՆԿՑԻԱ ՉԷ, քանի որ միայն այդպիսի ֆունկցիաներն են շրջելի: ? ԲԱՅՑ եթե խորանարդ ֆունկցիան ունի հետևյալ ձևը/կարող է փոխարկվել հետևյալ ձևի, այն շրջելի է՝ (i) f(x)=(ax+b)³+c, a≠0, b,c∈|R , իր բնական տիրույթով՝ x∈|R կամ կրճատված տիրույթով
Ի՞նչ է հակադարձ ֆունկցիան հաշվարկում:
Մաթեմատիկայի մեջ հակադարձ ֆունկցիան (կամ հակաֆունկցիան) մի ֆունկցիա է, որը «հակադարձում է» մեկ այլ ֆունկցիա. եթե x մուտքագրման վրա կիրառվող f ֆունկցիան տալիս է y-ի արդյունք, ապա դրա հակադարձ ֆունկցիան g-ին կիրառելով y-ին տալիս է x արդյունքը, և հակառակը, այսինքն՝ f(x) = y եթե և միայն եթե g(y) = x