Բովանդակություն:
Video: Ինչպե՞ս գրաֆիկորեն լուծել LP-ն Excel-ում:
2024 Հեղինակ: Miles Stephen | [email protected]. Վերջին փոփոխված: 2023-12-15 23:37
ՏԵՍԱՆՅՈՒԹ
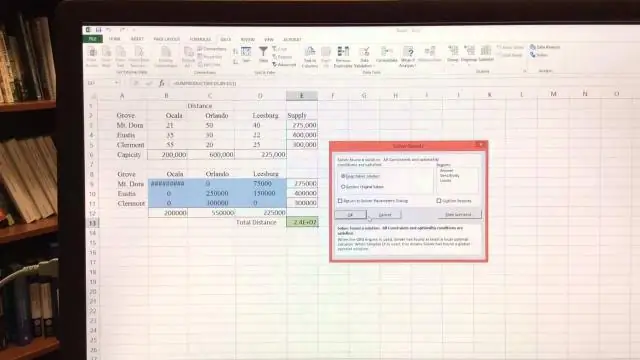
Այս կերպ ինչպե՞ս եք լուծում խնդիրը գրաֆիկորեն:
Դեպի լուծել հավասարումը նշանակում է գտնել բոլոր այն արժեքները, որոնք պնդում են ճշմարիտ: Դեպի լուծել մի հավասարում գրաֆիկորեն , գծեք հավասարման յուրաքանչյուր կողմի, անդամի գրաֆիկը և տեսեք, թե որտեղ են խաչվում կորերը, հավասար: Այս կետերի x արժեքները հավասարման լուծումներն են:
Բացի այդ, ինչպե՞ս եք լուծում իրագործելի տարածաշրջանը: Այն իրագործելի տարածաշրջան է շրջան գրաֆիկի, որը պարունակում է բոլոր կետերը, որոնք բավարարում են համակարգի բոլոր անհավասարությունները: Գրաֆիկական դարձնելու համար իրագործելի տարածաշրջան , նախ գծեք համակարգի յուրաքանչյուր անհավասարություն: Այնուհետև գտեք այն տարածքը, որտեղ բոլոր գրաֆիկները համընկնում են: դա է իրագործելի տարածաշրջան.
Նաև գիտեք, թե ինչպես կարելի է գտնել իրագործելի շրջանը գրաֆիկական մեթոդով:
Գրաֆիկական մեթոդ
- Քայլ 1. Ձևակերպեք LP (Գծային ծրագրավորում) խնդիրը:
- Քայլ 2. Կառուցեք գրաֆիկ և գծեք սահմանափակման գծերը:
- Քայլ 3. Որոշեք յուրաքանչյուր սահմանափակման տողի վավեր կողմը:
- Քայլ 4. Բացահայտեք իրագործելի լուծման տարածաշրջանը:
- Քայլ 5. Նպատակային ֆունկցիան գծեք գրաֆիկի վրա:
- Քայլ 6. Գտեք օպտիմալ կետը:
Ո՞րն է LPP-ի խնդիրը:
Սահմանում. Գծային ծրագրավորում խնդիր բաղկացած է գծային ֆունկցիայից, որը պետք է առավելագույնի հասցվի կամ նվազագույնի հասցվի՝ ենթարկվելով որոշակի սահմանափակումների՝ գծային հավասարումների կամ անհավասարությունների տեսքով:
Խորհուրդ ենք տալիս:
Ինչպե՞ս լուծել քառակուսի հավասարումը՝ օգտագործելով զրոյական գործոնի օրենքը:
Այստեղից կարող ենք եզրակացնել, որ եթե ցանկացած երկու թվի արտադրյալը զրո է, ապա թվերից մեկը կամ երկուսը զրո են: Այսինքն, եթե ab = 0, ապա a = 0 կամ b = 0 (որը ներառում է հնարավորություն, որ a = b = 0): Սա կոչվում է զրոյական գործոնի օրենք; և մենք հաճախ օգտագործում ենք այն քառակուսի հավասարումներ լուծելու համար
Ինչպե՞ս լուծել երկքայլ հավասարումները նախահանրահաշիվում:
ՏԵՍԱՆՅՈՒԹ Նմանապես, որո՞նք են հավասարումը լուծելու 4 քայլերը: Հավասարումների լուծման 4-քայլ ուղեցույց (մաս 2) Քայլ 1. Պարզեցնել հավասարման յուրաքանչյուր կողմը: Ինչպես նախորդ անգամ իմացանք, հավասարումը լուծելու առաջին քայլը հավասարումը հնարավորինս պարզեցնելն է:
Ինչպե՞ս լուծել կոտորակները բազմապատկելով և բաժանելով:
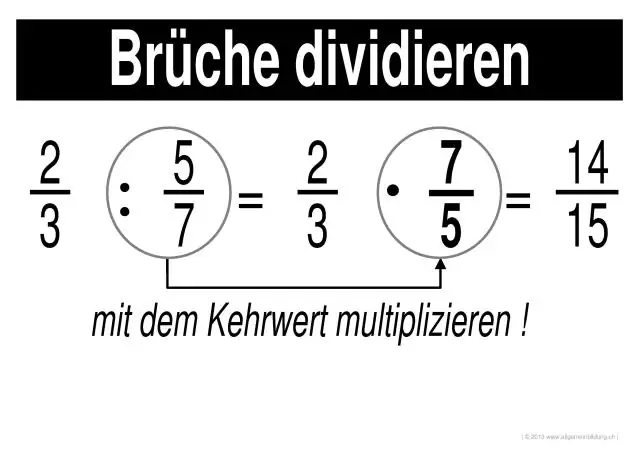
Կոտորակների բազմապատկում և բաժանում Քայլ 1. Յուրաքանչյուր կոտորակի համարիչները բազմապատկեք միմյանցով (վերևի թվերը): Արդյունքը պատասխանի համարիչն է։ Քայլ 2. Յուրաքանչյուր կոտորակի հայտարարները բազմապատկեք միմյանցով (ներքևի թվերը): Արդյունքը պատասխանի հայտարարն է։ Քայլ 3. Պարզեցնել կամ նվազեցնել պատասխանը
Ինչպե՞ս գրաֆիկորեն լուծել գծային հավասարումների համակարգը:
Գծային հավասարումների համակարգը գրաֆիկորեն լուծելու համար մենք երկու հավասարումները պատկերում ենք նույն կոորդինատային համակարգում: Համակարգի լուծումը կլինի երկու ուղիղների հատման կետում: Երկու ուղիղները հատվում են (-3, -4), որը հավասարումների այս համակարգի լուծումն է
Ինչպե՞ս լուծել Դեկարտի նշանների կանոնը:
Դեկարտի նշանների կանոնը մեզ ասում է, որ մենք ունենք ճիշտ 3 իրական դրական զրո կամ ավելի քիչ, բայց կենտ թվով զրո: Այսպիսով, մեր դրական զրոների թիվը պետք է լինի կամ 3, կամ 1: Այստեղ մենք կարող ենք տեսնել, որ մենք ունենք նշանների երկու փոփոխություն, հետևաբար մենք ունենք երկու բացասական զրո կամ պակաս, բայց զույգ թվով զրոներ: